

Kademeli azalma, türevi bilinmeyen veya analitik türev hesaplaması zor olan fonksiyonların minimum noktasının bulunmasına yarayan; makine öğrenimi için hayati öneme sahip bir optimizasyon algoritmasıdır. Doğrusal regresyon, lojistik regresyon, SVM, yapay sinir ağları ve derin öğrenme modelleri gibi pek çok makine öğrenmesi modeli kademeli azalma kullanılarak oluşturulmuştur.

Kaynak: https://typefully.com/xtinacomputes/gradient-descent-explained-sYiBK8Y
Kademeli azalma algoritmasının adımları aşağıdaki gibidir:

Kaynak: Coursera
- Fonksiyonda rastgele bir başlangıç noktası belirlenir.
- Üzerinde bulunulan noktanın türevi hesaplanır. Bu türev, fonksiyonun artış yönünün hangi yönde ve ne kadar büyüklükte olduğunu gösterir. Bu türeve gradyan denir.
- Düşüş yönüne doğru ne kadar mesafe ilerleneceğini belirlemek için bir adım boyutu belirlenir. Bu adım boyutuna öğrenme oranı(learning rate) denir. Öğrenme oranının doğru büyüklükte belirlenmesi, algoritmanın doğru çıktı vermesi için gereklidir.
- Öğrenme oranı ve gradyan çarpılır. Gradyanın, fonksiyonun artış yönünü gösterdiği ve kademeli azalma algoritmasının minimum noktaya doğru ilerle için bu çarpımın negatifi alınır.
- Elde edilen bu yeni gradyan, üzerinde bulunulan noktadan öğrenme oranı kadar uzaklıkta yeni bir noktaya ilerlemek için kullanılır.
- Eğer hedeflenen minimum noktaya yeterince yaklaşıldıysa veya belirlenen bir durdurma kriterine ulaşıldıysa algoritma amacını yerine getirmiştir, durur. Eğer istenilen sonuca ulaşılmadıysa adım ikiye geri dönülür.

Yerel ve Global Minimum Noktaları
Bazı fonksiyonlarda türevi sıfır olan birden fazla nokta bulunabilir. Fonksiyonun en küçük değeri aldığı noktaya “global minimum”, bu nokta dışında kalan türevi sıfır yapan çukurlara ise “yerel minimum” denir. Algoritmanın kullanılma amacı global minimuma ulaşmaktır ve işlem yaparken yerel minimuma takılmak istenmeyen bir sonuçtur.

Kaynak: https://www.mltut.com/stochastic-gradient-descent-a-super-easy-complete-guide/

Kaynak: https://blog.paperspace.com/intro-to-optimization-in-deep-learning-gradient-descent/
Öğrenme Oranının Algoritmaya Etkisi
1. Öğrenme Oranı Fazla Küçük Olursa:
Öğrenme oranı ne kadar küçük olursa, algoritmanın minimum noktaya ulaşana kadar atacağı adım da sayısı o kadar artar, dolayısıyla algoritma o kadar yavaş çalışır. Ayrıca atılacak adımların boyutları küçük olacağından, algoritma yerel bir minimum noktasında takılı kalabilir. Böylece global minimum noktasına ulaşılamaz ve algoritma doğru çalışmamış olur. Bunun yerine daha büyük bir öğrenme oranı seçilirse algoritma yerel minimum noktasının üzerinden atlayabilir ve global minimuma ulaşabilir.

Kaynak: https://towardsdatascience.com/an-intuitive-explanation-of-gradient-descent-83adf68c9c33
2. Öğrenme Oranı Fazla Büyük Olursa:
Algoritmanın hızlı çalışması ve bilgisayarı daha az yorması için öğrenme oranının olabildiğince yüksek olması istenir. Ancak öğrenme oranı fazla büyük alınırsa algoritma aşırı büyük adım attığı için sürekli olarak global minmum noktasının üzerinden geçer ve fonksiyonun minimum değer aldığı noktayı asla yakalayamaz. Bu duruma “over-shooting” denir.
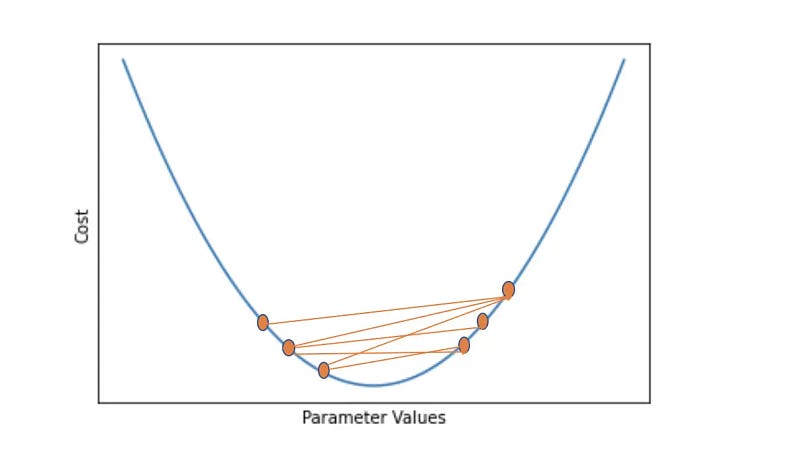

Kaynak: https://blog.paperspace.com/intro-to-optimization-in-deep-learning-gradient-descent/
Öğrenme oranının kademeli azalmaya etkisini, Google Developers’dan animasyonlu olarak inceleyebilirsiniz:
Reducing Loss: Optimizing Learning Rate | Machine Learning | Google for Developers
Estimated Time: 15 minutes Set a learning rate of 0.03 on the slider. Keep hitting the STEP button until the gradient…

Kaynak: https://saugatbhattarai.com.np/what-is-gradient-descent-in-machine-learning/

Kaynak: https://towardsdatascience.com/gradient-descent-explained-9b953fc0d2c
Kademeli Azalmanın Doğrusal Regresyona Uygulanması
Doğrusal regresyon, bir bağımlı değişken ile bir veya daha fazla bağımsız değişken arasındaki ilişkiyi anlamlandırmak ve bu ilişkiyi doğrusal bir çizgi ile temsil ederek tahminleme yapmaya yarayan istatistiksel bir yöntemdir.

Kaynak: https://www.unite.ai/simple-linear-regression-in-the-field-of-data-science/
Makine öğrenmesi modellerini optimize ederken, modelin ne kadar doğru olduğunu gösteren ve böylece kademeli azalma ile optimuma ulaşmaya olanak tanıyan fonksiyonlara “maliyet fonksiyonu” denir. Maliyet fonksiyonu minimize edildiğinde optimum modele ulaşılmış olunur. Bu örnekte kare hata maliyet fonksiyonu kullanılmıştır. “Kare hata maliyet fonksiyonu”, çizilen doğrusal tahmin çizgisi ile her bir gerçek veri arasındaki uzaklığın kareleri toplamının kareköküne eşittir.
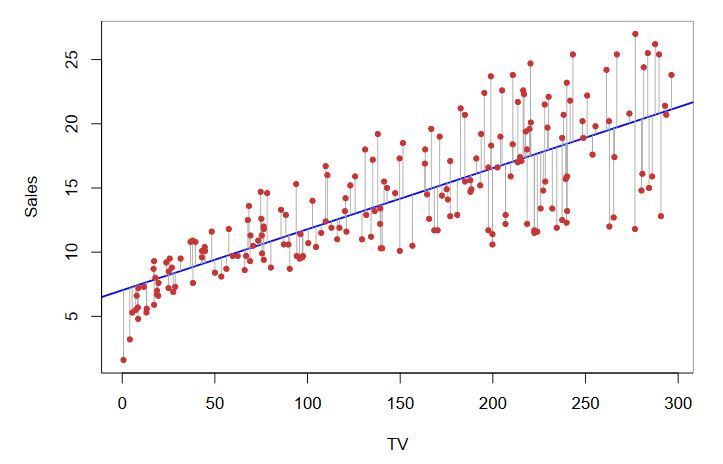
Kaynak: https://web.stanford.edu/class/stats202/notes/Linear-regression/Simple-linear-regression.html
Doğrusal regresyon konveks(iç bükey) bir fonksiyon olduğu için yerel minimum nokta bulunmaz ve doğrudan global minimuma ulaşılır.
Kademeli azalma, doğrusal regresyon ve kare hata maliyet fonksiyonlarının formülleri ayrı ayrı aşağıda verilmiştir:

Kaynak: https://medium.com/@Shreedharvellay/gradient-descent-for-linear-regression-8e1389058d07
Kademeli azalmayı doğrusal regresyon formülünde yerine koyarsak aşağıdaki formüle ulaşırız:

Algoritmanın doğru bir biçimde çalışması için teta 0 ve teta 1 değerlerinin adım başı eş zamanlı ve sürekli olarak güncellenmesi gerekmektedir.
Maliyet fonksiyonunda minimuma doğru doğru atılan her adımda, doğrusal regresyon doğrusu daha optimum bir konuma hareket edecektir.

Kaynak: https://wingshore.wordpress.com/2014/11/20/gradient-descent-for-linear-regression/
Kademeli Azalmaya Farklı Bir Yaklaşım
1. Geleneksel Kademeli Azalma(Batch Gradient Descent-BGD)
Yukarıdaki doğrusal regresyon modelinde yapıldığı gibi öğrenme verisinin sürekli olarak, atılan adım başı güncellendiği kademeli azalma tipine “geleneksel kademeli azalma” denir. Ancak bu yöntemin, konveks olmayan bir fonksiyon üzerinde yerel bir minimum noktasına takılı kalma ihtimali yüksektir, ayrıca tüm öğrenme verisini işleme aldığından daha büyük verilerde yavaş çalışır.
Geleneksel kademeli azalma gerçek hayatta pek tercih edilmese de genel olarak aşağıdaki modellere uygulanabilir:
a. Doğrusal regresyon
b. Lojistik regresyon
c. Karar ağaçları
d. Destek vektör makineleri(SVM)
e. Doğrusal diskriminant analizi(LDA)
Not: Geleneksel kademeli azalmanın yukarıdaki modellere uygulanması her ne kadar mümkün olsa da, eğer büyük bir veri setiyle uğraşılıyorsa maliyet açısından diğer kademeli azalma tipleri tercih edilir
2. Rastgele Kademeli Azalma(Stochastic Gradient Descent-SGD)
Rastgele kademeli azalma, geleneksel kademeli azalmadan farklı olarak, her adımda sadece bir veriyi rastgele seçerek hesaplama yapar. Bu sayede eğitim sürecinde tüm veriler kullanılmaz ve zamandan ve bellekten tasarruf edilmiş olunur.
Rastgele kademeli azalmanın adımları aşağıdaki gibidir:
- Modelin parametreleri rastgele değerlerle başlatılır.
- Veri kümesinden rastgele bir örnek seçilir.
- Seçilen örneğe göre maliyet fonksiyonunun gradyanı hesaplanır ve öğrenme katsayısıyla çarpılır.
- Gradyanın zıttı yönünde adım atılır ve tanımlanan şartlar sağlanmadıysa adım ikiye dönülür.
Rastgele kademeli azalma her ne kadar büyük veri setleri karmaşık modeller üzerinde kullanıldığunda etkili sonuçlar verse de gradyan hesaplamaları rastgele örneklerle yapıldığı için eğitim süreci düzensiz ve gürültülü olabilir.
Büyük veri setlerinin yanında aşağıdaki modellerde geleneksel kademeli azalma yerine rastgele kademeli azalma kullanılması sağlıklı olacaktır:
a. Derin öğrenme modelleri (CNN ve RNN gibi.)
b. Online öğrenme ve güncellenen veriler.
c. Dizisel veriler (Doğal dil işleme ve zaman serileri gibi.)

Kaynak: https://yakout.io/deeplearning/coursera-deep-learning-course-2-week-2/
Kaynakça
- Makine Öğrenmesi Eğitimi, Musa Arda, Udemy
- Gradient Descent(Kademeli Azalma) 1–2–3, Özkan Yılmaz, Youtube
- https://medium.com/analytics-vidhya/gradient-descent-and-beyond-ef5cbcc4d83e
- https://towardsdatascience.com/batch-mini-batch-stochastic-gradient-descent-7a62ecba642a
- https://hritikaa9.medium.com/gradient-descent-for-linear-regression-171369a5d66e
- https://www.youtube.com/watch?v=vMh0zPT0tLI
- ChatGPT :)