

Makine öğrenmesi projelerinde metrikler, model performansını değerlendirmek ve kararlar almak için kritik öneme sahiptir. Her metriğin belirli bir amacı ve kullanım senaryosu vardır. Örneğin, Doğruluk (Accuracy), genel model performansını hızlı bir şekilde ölçmek için kullanışlıdır, ancak sınıf dengesizliği durumlarında yanıltıcı olabilir. Kesinlik (Precision), false positive hatalarını minimize etmek istediğiniz durumlarda önemlidir, örneğin, spam filtresi uygulamalarında. Duyarlılık (Recall), false negative hatalarını en aza indirmek istediğiniz durumlarda önemlidir, özellikle hastalık teşhisi gibi. F1-Skoru, kesinlik ve duyarlılık arasındaki dengeyi sağlamak için kullanılır ve dengesiz sınıf dağılımları için uygundur. Karışıklık Matrisi, farklı hata türlerini anlamak ve görselleştirmek için kullanılır. ROC Eğrisi ve AUC, sınıfları ayırt etme yeteneğini görselleştirmek için kullanılır. Logaritmik Kayıp, olasılık tahminlerinin doğruluğunu ölçer. MAE ve MSE, regresyon modelleri için tahmin hatalarını değerlendirir. R-Kare, regresyon modellerinin açıklanabilirlik derecesini ölçer. Doğruluk Çapraz Doğrulama, modelin performansını daha güvenilir bir şekilde değerlendirmek için kullanılır. Hangi metriğin kullanılacağı, veri setinin özelliklerine, iş problemine ve hedeflere bağlıdır. Dolayısıyla, veri bilimcileri ve mühendisler, metrikleri dikkatle seçmeli ve model performansını değerlendirirken bu metrikleri birlikte kullanarak daha kapsamlı bir anlayış elde etmelidir.

Doğruluk (Accuracy):
Makine öğrenmesi, günümüzün veri zengini dünyasında büyük bir rol oynamaktadır. Bu teknoloji, veri analizi, tahminler, sınıflandırmalar ve regresyon gibi birçok uygulama alanında kullanılır. Ancak, bir makine öğrenimi modelinin gerçek dünya performansını değerlendirmek ve iyileştirmek için kullanılan metrikler arasında doğruluk (Accuracy) özel bir öneme sahiptir. Bu makalede, doğruluk metriğini ayrıntılı bir şekilde ele alacağız ve ne zaman kullanılması gerektiği, ne zaman yetersiz kalabileceği konularını tartışacağız.
Doğruluk, bir sınıflandırma modelinin doğru tahminlerinin, tüm veri noktalarına göre yüzdesini hesaplayan temel bir metriktir. Bu, bir modelin performansını bir bakışta değerlendirmenizi sağlar. Doğruluk hesaplamak için, doğru tahmin edilen veri noktalarının toplam sayısını toplam veri noktalarının sayısına bölersiniz. Formül şu şekildedir:
Doğruluk (Accuracy) = (Doğru Tahminler) / (Toplam Veri Sayısı)
Bir örnek senaryo üzerinden ilerleyelim. Diyelim ki bir sınıflandırma modeli, 100 örnek içeren bir veri kümesinde çalışıyor ve bu model, bu örneklerin 85’ini doğru bir şekilde sınıflandırıyor. Bu durumda, doğruluk hesaplama şekli şu şekilde olacaktır: 85 / 100 = 0.85 veya %85 doğruluk değerine sahipsiniz.
Yüksek doğruluk genellikle daha iyi bir model performansını gösterir. Ancak, doğruluk metriği her zaman en uygun metrik olmayabilir. İşte dikkate almanız gereken bazı durumlar:
1. Dengesiz Sınıf Dağılımları: Eğer sınıflar arasında büyük bir dengesizlik varsa, doğruluk metriği yetersiz olabilir. Örneğin, %95 — %5 gibi bir dengesizlik durumunda, model çoğunluk sınıfını tahmin ederek yüksek doğruluk elde edebilirken, azınlık sınıfını doğru tahmin etmemiş olabilir.
2. Sınıf Dengesizliği ve Yanıltıcılık: Eğer bir sınıf daha az yaygınsa ve bu sınıfı yanlış tahmin etmek ciddi sonuçlara yol açıyorsa, doğruluk metriği yanıltıcı olabilir. Daha duyarlı metrikler (kesinlik, duyarlılık, F1-Skoru) tercih edilmelidir.
3. Başka Metrikler: Veri setinin özelliğine ve problem türüne göre, doğruluk yerine başka metrikler daha anlamlı olabilir. Örneğin, tıbbi bir teşhis problemi gibi durumlarda duyarlılık (recall) daha kritik olabilir.
Sonuç olarak, doğruluk metriği, bir modelin genel performansını değerlendirmek için kullanışlı bir başlangıç noktasıdır. Ancak, her zaman dikkatli bir şekilde kullanılmalı ve veri setinin ve problem türünün gereksinimlerini göz önünde bulundurmalısınız. İhtiyaca göre diğer metriklerle birlikte kullanılmalıdır.
import numpy as np
from sklearn.metrics import accuracy_score
# Örnek veri oluşturalım
np.random.seed(42)
y_true = np.random.randint(2, size=100) # Gerçek sınıflar (0 veya 1)
y_pred = np.random.randint(2, size=100) # Model tahminleri (0 veya 1)
# Doğruluk (Accuracy) hesaplama
accuracy = accuracy_score(y_true, y_pred)
print("Doğruluk:", accuracy)
Doğruluk: 0.5
Kesinlik (Precision):
Kesinlik, bir sınıflandırma modelinin pozitif olarak tahmin ettiği örneklerin gerçekten pozitif olduğu oranıdır. Yani, kesinlik bir modelin pozitif tahminlerinin ne kadarının gerçek pozitif olduğunu ölçer. Formülü şu şekildedir:

Kesinlik (Precision) = (Gerçek Pozitif) / (Gerçek Pozitif + Yanlış Pozitif)
Bu metrik, false positive hatalarının sınırlanması gereken durumlarda kritik bir rol oynar. Örneğin, bir spam filtresi uygulamasında, gerçek e-postaların yanlışlıkla spam olarak işaretlenmesi istenmez. Kesinlik, bu yanlış pozitiflerin sayısını azaltarak bu tür hataları önlemeye yardımcı olur.
Kesinlik ile Doğruluk Arasındaki Fark
Kesinlik (Precision) metriği, doğruluk (Accuracy) metriğinden önemli bir fark taşır. Doğruluk, tüm doğru tahminlerin oranını hesaplar, ancak kesinlik yalnızca pozitif olarak tahmin edilenlerin doğruluğunu ölçer. Yani, doğruluk, negatif tahminler dahil tüm tahminleri kapsarken, kesinlik yalnızca pozitif tahminleri değerlendirir.
from sklearn.metrics import precision_score
# Örnek veri oluşturalım
y_true = [1, 1, 0, 1, 0, 0, 1, 0, 1, 1]
y_pred = [1, 0, 0, 1, 1, 0, 1, 1, 1, 1]
# Kesinlik (Precision) hesapla
precision = precision_score(y_true, y_pred)
print("Kesinlik (Precision):", precision)
Kesinlik (Precision): 0.7142857142857143
Duyarlılık (Recall veya Sensitivity):
Makine öğrenmesi ve sınıflandırma problemleri, genellikle başarının bir ölçüsü olarak doğruluk (Accuracy) metriği ile değerlendirilir. Ancak, bazı durumlarda doğruluk yetersiz kalabilir ve özellikle gerçek pozitiflerin önemli olduğu durumlarda devreye duyarlılık (Recall veya Sensitivity) metriği girer.
Duyarlılık (Recall) Nedir?
Duyarlılık, gerçek pozitif örneklerin ne kadarının pozitif olarak tahmin edildiğini ölçer. Yani, duyarlılık bir modelin gerçek pozitifleri ne kadar yakaladığını gösterir. Formülü şu şekildedir:

Duyarlılık (Recall) = (Gerçek Pozitif) / (Gerçek Pozitif + Yanlış Negatif)
Duyarlılık, özellikle hastalık teşhisi gibi durumlarda hastalığın kaçırılmaması gereken kritik bir metriktir. Yanlış negatifler, gerçek pozitifleri kaçırmaktan kaynaklanır ve bu tür hataların maliyeti veya tehlikesi yüksek olduğunda duyarlılık öne çıkar.
Duyarlılık ile Doğruluk Arasındaki Fark
Duyarlılık (Recall) metriği, doğruluk (Accuracy) metriğinden önemli bir fark taşır. Doğruluk, tüm doğru tahminlerin oranını hesaplar, ancak duyarlılık yalnızca gerçek pozitifleri değerlendirir. Yani, doğruluk, negatif tahminler dahil tüm tahminleri kapsarken, duyarlılık yalnızca pozitif tahminleri değerlendirir.
from sklearn.metrics import recall_score
# Örnek veri oluşturalım
y_true = [1, 1, 0, 1, 0, 0, 1, 0, 1, 1]
y_pred = [1, 0, 0, 1, 1, 0, 1, 1, 1, 1]
# Duyarlılık (Recall) hesapla
recall = recall_score(y_true, y_pred)
print("Duyarlılık (Recall):", recall)
Duyarlılık (Recall): 0.8333333333333334
F1 Score
F1-Skoru, bir sınıflandırma modelinin kesinlik (Precision) ve duyarlılık (Recall) arasındaki dengeyi sağlamak için kullanılan bir metriktir. Yüksek kesinlik ve yüksek duyarlılık bir arada aranıyorsa, F1-Skoru bu dengeyi sağlamak için kullanışlıdır. Formülü şu şekildedir:
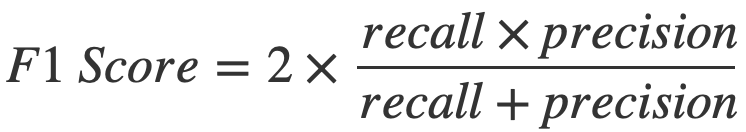
F1-Skoru = 2 * (Kesinlik * Duyarlılık) / (Kesinlik + Duyarlılık)
F1-Skoru, özellikle dengesiz sınıf dağılımlarıyla başa çıkmak için kullanışlıdır. Dengesiz veri kümelerinde, doğruluk metriği yanıltıcı olabilir çünkü çoğunluk sınıfını tahmin ederek yüksek bir doğruluk elde edilebilirken, azınlık sınıfının performansı göz ardı edilebilir. F1-Skoru, bu tür durumlarda performansı daha adil bir şekilde değerlendirmenize yardımcı olur.
F1-Skoru ile Doğruluk Arasındaki Fark
F1-Skoru, doğruluk (Accuracy) metriğinden önemli bir fark taşır. Doğruluk, tüm doğru tahminlerin oranını hesaplar, ancak F1-Skoru, kesinlik (Precision) ve duyarlılık (Recall) arasındaki dengeyi ölçer. Yani, doğruluk, negatif tahminler dahil tüm tahminleri kapsarken, F1-Skoru pozitif tahminlerin doğruluğu ve eksikliği arasındaki dengeyi değerlendirir.
from sklearn.metrics import f1_score
from sklearn.metrics import precision_score, recall_score
# Örnek veri oluşturalım
y_true = [1, 1, 0, 1, 0, 0, 1, 0, 1, 1]
y_pred = [1, 0, 0, 1, 1, 0, 1, 1, 1, 1]
# Kesinlik (Precision) ve Duyarlılık (Recall) hesapla
precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
# F1-Skoru hesapla
f1 = f1_score(y_true, y_pred)
print("Kesinlik (Precision):", precision)
print("Duyarlılık (Recall):", recall)
print("F1-Skoru:", f1)
Kesinlik (Precision): 0.7142857142857143
Duyarlılık (Recall): 0.8333333333333334
F1-Skoru: 0.7692307692307692
Karışıklık Matrisi (Confusion Matrix)
Makine öğrenmesi ve sınıflandırma problemleri, genellikle doğruluk (Accuracy), kesinlik (Precision), duyarlılık (Recall), ve F1-Skoru gibi metriklerle değerlendirilir. Ancak, sınıflandırma modelinizin performansını daha derinlemesine anlamak ve hataları görsel olarak görmek istiyorsanız, Karışıklık Matrisi (Confusion Matrix) kullanışlı bir araçtır.
Karışıklık Matrisi Nedir?
Karışıklık Matrisi, sınıflandırma modelinizin performansını görsel olarak temsil eden bir matristir. Bu matris, gerçek sınıflar ve tahmin edilen sınıflar arasındaki ilişkiyi gösterir. Genellikle 2x2 matris olarak temsil edilir ve dört farklı hata türünü açıkça gösterir:

True Positive (TP): Gerçek pozitif örneklerin doğru bir şekilde pozitif olarak tahmin edildiği durumlar.
True Negative (TN): Gerçek negatif örneklerin doğru bir şekilde negatif olarak tahmin edildiği durumlar.
False Positive (FP): Gerçek negatif örneklerin yanlışlıkla pozitif olarak tahmin edildiği durumlar.
False Negative (FN): Gerçek pozitif örneklerin yanlışlıkla negatif olarak tahmin edildiği durumlar.
Karışıklık Matrisi ile Ne Yapabilirsiniz?
Karışıklık Matrisi, sınıflandırma modelinizin performansını daha iyi anlamanıza yardımcı olabilir. İşte bazı kullanışlı işlevleri:
Hata Analizi: Modelinizin hangi tür hatalar yaptığını daha iyi anlayabilirsiniz. Özellikle false positive ve false negative hatalarını görsel olarak incelemek, modelinizi iyileştirmek için ipuçları sunabilir.
Sınıf Dengesizliği: Dengesiz sınıf dağılımlarıyla başa çıkmak için kullanışlıdır. Model, çoğunluk sınıfını tahmin ederek yüksek bir doğruluk elde edebilirken, azınlık sınıfını doğru tahmin etmemiş olabilir.
İlgili Metriklerin Hesaplanması: Karışıklık matrisi, kesinlik (Precision), duyarlılık (Recall), F1-Skoru ve diğer metriklerin hesaplanmasına yardımcı olur.
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
# Örnek veri oluşturalım
y_true = [1, 1, 0, 1, 0, 0, 1, 0, 1, 1]
y_pred = [1, 0, 0, 1, 1, 0, 1, 1, 1, 1]
# Karışıklık Matrisi (Confusion Matrix) hesapla
conf_matrix = confusion_matrix(y_true, y_pred)
print("Karışıklık Matrisi:")
print(conf_matrix)
# Görselleştirme
def plot_confusion_matrix(conf_matrix):
plt.imshow(conf_matrix, interpolation='nearest', cmap=plt.get_cmap('Blues'))
plt.title('Karışıklık Matrisi')
plt.colorbar()
plt.xticks([0, 1], ['Tahmin Edilen 0', 'Tahmin Edilen 1'])
plt.yticks([0, 1], ['Gerçek 0', 'Gerçek 1'])
plt.xlabel('Tahminler')
plt.ylabel('Gerçek Değerler')
plot_confusion_matrix(conf_matrix)
plt.show()
Karışıklık Matrisi:
[[2 2]
[1 5]]

ROC Eğrisi ve AUC
Makine öğrenmesi ve sınıflandırma problemleri, doğruluk (Accuracy), kesinlik (Precision), duyarlılık (Recall), ve F1-Skoru gibi metriklerle değerlendirilir. Ancak, modelinizin farklı kesme noktalarında performansını ve sınıfları ayırt etme yeteneğini görsel olarak anlamak istiyorsanız, ROC Eğrisi (Receiver Operating Characteristic) ve AUC (Alan Altındaki Eğri) metrikleri işinize yarayabilir.
ROC Eğrisi ve AUC Nedir?
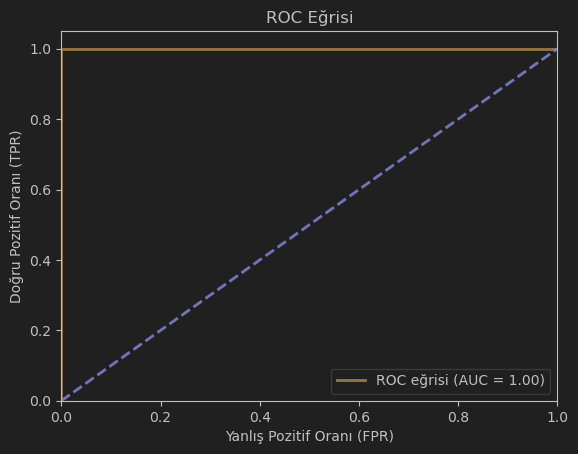
ROC Eğrisi (Receiver Operating Characteristic): ROC eğrisi, bir sınıflandırma modelinin farklı kesme noktalarında duyarlılık ve özgüllüğünü görselleştirir. Duyarlılık, gerçek pozitif oranını, özgüllük ise gerçek negatif oranını temsil eder. ROC eğrisi, bu iki metriği kesme noktasına göre farklılaştırarak modelin performansını çizgisel olarak gösterir. Bir modelin ROC eğrisi, sol üst köşeye ne kadar yakınsa, o kadar iyi performans gösterir.
AUC (Alan Altındaki Eğri): AUC, ROC eğrisinin altındaki alanı ölçer. Bu metrik, bir modelin sınıfları ayırt etme yeteneğini değerlendirmek için kullanılır. AUC değeri 1’e yaklaştıkça, model daha iyi performans gösterir.

ROC Eğrisi ve AUC ile Ne Yapabilirsiniz?
Model Karşılaştırma: Farklı sınıflandırma modellerini karşılaştırmak için ROC eğrisi ve AUC kullanabilirsiniz. AUC değeri yüksek olan model, sınıfları daha iyi ayırt edebilir.
Kesme Noktası Seçimi: ROC eğrisi, farklı kesme noktalarında duyarlılık ve özgüllüğü gösterdiğinden, modelinize en uygun kesme noktasını seçebilirsiniz. İşinize en uygun dengeyi sağlamak için ROC eğrisini kullanabilirsiniz.
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
# Örnek veri oluşturalım
y_true = [1, 1, 0, 1, 0, 0, 1, 0, 1, 1]
y_scores = [0.9, 0.8, 0.3, 0.7, 0.2, 0.4, 0.6, 0.5, 0.8, 0.7]
# ROC eğrisi hesapla
fpr, tpr, thresholds = roc_curve(y_true, y_scores)
# AUC hesapla
roc_auc = auc(fpr, tpr)
print("AUC (Alan Altındaki Eğri):", roc_auc)
# ROC eğrisini görselleştir
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC eğrisi (AUC = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('Yanlış Pozitif Oranı (FPR)')
plt.ylabel('Doğru Pozitif Oranı (TPR)')
plt.title('ROC Eğrisi')
plt.legend(loc="lower right")
plt.show()
AUC (Alan Altındaki Eğri): 1.0
Logaritmik Kayıp (Log Loss)
Sınıflandırma problemlerinde, doğru tahminlerin yanı sıra olasılık tahminlerinin doğruluğu da önemlidir. Logaritmik Kayıp (Log Loss), bu olasılık tahminlerinin doğruluğunu ölçen bir metriktir. Log kaybı ne kadar düşükse, modelin olasılık tahminleri o kadar iyi olur. Bu yazıda, Logaritmik Kayıp metriğini daha ayrıntılı bir şekilde inceleyeceğiz.
Logaritmik Kayıp Nedir?
Logaritmik Kayıp (Log Loss), olasılık tahminlerinin gerçek sınıf etiketleriyle ne kadar uyumlu olduğunu ölçen bir metriktir. Bu metrik, her bir örnek için tahmin edilen olasılık dağılımını ve gerçek sınıf etiketini kullanır. Log kaybı, olasılıkların gerçek etiketlere ne kadar yakın olduğunu hesaplar.
Log Loss’un formülü şu şekildedir:
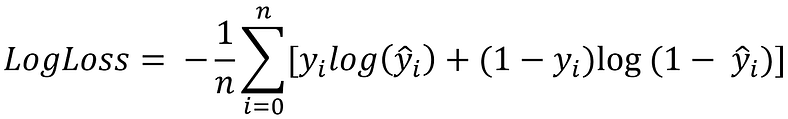
Log Loss = -1/n * Σ(y * log(p) + (1-y) * log(1-p))
Burada:
n, örnek sayısını temsil eder.
y, gerçek sınıf etiketini (0 veya 1) temsil eder.
p, tahmin edilen olasılığı temsil eder.
Log Loss, her bir örnek için hesaplanır ve ardından bu değerlerin ortalaması alınır.
Logaritmik Kayıp ile Ne Yapabilirsiniz?
Model Karşılaştırma: Farklı sınıflandırma modellerini karşılaştırmak için Log Loss’u kullanabilirsiniz. Daha düşük Log Loss değerine sahip model, olasılık tahminlerini daha iyi yapar.
Kesme Noktası Seçimi: Log Loss, sınıflandırma modellerinde kullanılan kesme noktalarını ayarlamak için de kullanışlıdır. Modelinizin kesme noktasını ayarlayarak Log Loss’u optimize edebilirsiniz.
from sklearn.metrics import log_loss
# Örnek veri oluşturalım
y_true = [1, 0, 1, 0, 1]
y_prob = [0.9, 0.2, 0.8, 0.3, 0.7]
# Log Loss hesapla
logloss = log_loss(y_true, y_prob)
print("Log Loss:", logloss)
Log Loss: 0.2529995012327421
Ortalama Mutlak Hata (Mean Absolute Error)
Regresyon modelleri, gerçek sayısal değerleri tahmin etmek için kullanılır. Bu modellerin performansını değerlendirmek için kullanılan iki temel metrik, Ortalama Mutlak Hata (MAE) ve Ortalama Kare Hata (MSE) metrikleridir. Bu yazıda, MAE ve MSE metriklerini daha ayrıntılı bir şekilde inceleyeceğiz.
Ortalama Mutlak Hata (MAE) Nedir?
Ortalama Mutlak Hata (MAE), bir regresyon modelinin tahminlerinin gerçek değerlerden mutlak farklarının ortalamasını hesaplayan bir metriktir. MAE, modelin tahminlerinin gerçek değerlere ne kadar yakın olduğunu ölçer. MAE’nin formülü şu şekildedir:

MAE = 1/n * Σ|y — ŷ|
Burada:
n, örnek sayısını temsil eder.
y, gerçek değeri temsil eder.
ŷ, modelin tahmin ettiği değeri temsil eder.
MAE, her bir örnek için hesaplanır ve ardından bu değerlerin ortalaması alınır.
Ortalama Kare Hata (MSE) Nedir?
Ortalama Kare Hata (MSE), bir regresyon modelinin tahminlerinin gerçek değerlerden kare farklarının ortalamasını hesaplayan bir metriktir. MSE, büyük hataların küçük hatalarla dengelendiği bir metriktir. MSE’nin formülü şu şekildedir:

MSE = 1/n * Σ(y — ŷ)²
MAE gibi, n örnek sayısını, y gerçek değeri ve ŷ modelin tahmin ettiği değeri temsil eder.
MAE ve MSE ile Ne Yapabilirsiniz?
Model Karşılaştırma: Farklı regresyon modellerini karşılaştırmak için MAE ve MSE’yi kullanabilirsiniz. Daha düşük MAE veya MSE değerine sahip model, daha iyi tahminler yapar.
Model İyileştirme: MAE ve MSE, modelin hatalarını anlamak ve iyileştirmek için kullanılabilir. Hangi örneklerin daha fazla hata yaptığını belirleyebilirsiniz.
from sklearn.metrics import mean_absolute_error, mean_squared_error
import numpy as np
# Örnek veri oluşturalım
y_true = np.array([3.5, 2.0, 6.8, 7.5, 4.2])
y_pred = np.array([3.2, 1.8, 6.6, 7.0, 4.0])
# MAE hesapla
mae = mean_absolute_error(y_true, y_pred)
print("MAE (Ortalama Mutlak Hata):", mae)
# MSE hesapla
mse = mean_squared_error(y_true, y_pred)
print("MSE (Ortalama Kare Hata):", mse)
MAE (Ortalama Mutlak Hata): 0.28
MSE (Ortalama Kare Hata): 0.092
R-Kare (R-Squared)
Regresyon modelleri, gerçek sayısal değerleri tahmin etmek için kullanılır. Modelin verileri ne kadar iyi açıkladığını ölçmek için kullanılan önemli bir metrik, R-Kare (R-Squared) metriğidir. Bu yazıda, R-Kare metriğini daha ayrıntılı bir şekilde inceleyeceğiz.
R-Kare (R-Squared) Nedir?
R-Kare (R-Squared), bir regresyon modelinin açıklanabilirlik derecesini ölçen bir metriktir. R-Kare değeri, modelin veri setindeki değişkenliği ne kadar iyi açıkladığını gösterir. R-Kare değeri 0 ile 1 arasında bir değer alır.
R-Kare’nin hesaplama yöntemi şu şekildedir:

R-Kare = 1 — (Toplam Kareler Regresyon / Toplam Kareler Toplamı)
Burada:
Toplam Kareler Regresyon, regresyon modelinin tahminleri ile veri setinin ortalaması arasındaki kare farkların toplamını temsil eder.
Toplam Kareler Toplamı, veri setinin her bir örneğinin gerçek değeri ile veri setinin ortalaması arasındaki kare farkların toplamını temsil eder.
R-Kare değeri 1’e ne kadar yakınsa, model veri setini o kadar iyi açıklar.
R-Kare ile Ne Yapabilirsiniz?
Model Değerlendirme: R-Kare, farklı regresyon modellerini değerlendirmek için kullanılabilir. Daha yüksek R-Kare değerine sahip model, verileri daha iyi açıklar.
Model İyileştirme: R-Kare, modelin açıklanabilirlik derecesini anlamak ve iyileştirmek için kullanılır. R-Kare değerini artırmak için modelinizi geliştirebilirsiniz.
from sklearn.metrics import r2_score
import numpy as np
# Örnek veri oluşturalım
y_true = np.array([3.5, 2.0, 6.8, 7.5, 4.2])
y_pred = np.array([3.2, 2.1, 6.6, 7.0, 4.0])
# R-Kare hesapla
r2 = r2_score(y_true, y_pred)
print("R-Kare (R-Squared):", r2)
R-Kare (R-Squared): 0.9796978281397545
Doğruluk Çapraz Doğrulama (Accuracy Cross-Validation)
Makine öğrenimi modellerinin performansını doğru bir şekilde değerlendirmek, genellikle Doğruluk Çapraz Doğrulama (Cross-Validation) yöntemi ile yapılır. Bu yöntem, modelin istikrarını ve genelleme yeteneğini ölçmek için kullanılır. Bu yazıda, Doğruluk Çapraz Doğrulama yöntemini daha ayrıntılı bir şekilde inceleyeceğiz.
Doğruluk Çapraz Doğrulama Nedir?
Doğruluk Çapraz Doğrulama (Cross-Validation), veriyi farklı parçalara bölerek modelin performansını değerlendirmenin bir yöntemidir. Veri kümesi rastgele alt veri kümelerine ayrılır ve model, her bir alt küme üzerinde eğitilir ve diğer alt kümeler üzerinde test edilir. Bu işlem, tüm alt kümeler üzerinde tekrarlanır ve sonuçlar ortalaması alınır.

Klasik çapraz doğrulama yöntemlerinden biri, k-fold çapraz doğrulamadır. Bu yöntemde veri kümesi rastgele k alt kümelere bölünür. Model, k-1 alt küme üzerinde eğitilir ve bir alt küme üzerinde test edilir. Bu işlem, her bir alt küme için tekrarlanır.
Doğruluk Çapraz Doğrulama ile Ne Yapabilirsiniz?
Model Değerlendirme: Doğruluk Çapraz Doğrulama, modelin performansını daha güvenilir bir şekilde değerlendirmenize yardımcı olur. Birden fazla test seti kullanarak modelin konsistansını ölçebilirsiniz.
Veri Miktarının Etkisi: Doğruluk Çapraz Doğrulama, sınırlı veri miktarı durumunda model performansını değerlendirmek için de kullanışlıdır. Veri kümesini verimli bir şekilde kullanmanıza yardımcı olur.
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
# Örnek veri kümesi yükleme
data = load_iris()
X, y = data.data, data.target
# Model oluşturma
model = RandomForestClassifier()
# 5-fold çapraz doğrulama ile modeli değerlendirme
scores = cross_val_score(model, X, y, cv=5)
# Sonuçları görüntüleme
print("Çapraz Doğrulama Sonuçları:", scores)
print("Ortalama Doğruluk:", scores.mean())
Çapraz Doğrulama Sonuçları: [0.96666667 0.96666667 0.93333333 0.93333333 1. ]
Ortalama Doğruluk: 0.96
Bu yazıda, makine öğrenmesi modellerinin performansını değerlendirmek için kullanılan temel metrikleri ve yöntemleri inceledik. Doğruluk, kesinlik, duyarlılık, F1-Skoru, karışıklık matrisi, ROC eğrisi, logaritmik kayıp, MAE, MSE, R-Kare ve doğruluk çapraz doğrulama gibi metriklerin her biri, model performansını farklı yönleriyle değerlendirmemize yardımcı olur. Hangi metriği seçeceğiniz, probleminizin türüne, veri dağılımına ve hedefinize bağlıdır. Ayrıca, bu metriklerin iş probleminiz için anlamlı olup olmadığını dikkate almalısınız. Doğru metrikleri seçmek, veri bilimcileri ve mühendisler için kritik bir adımdır ve modelinizi daha iyi anlamalarına ve iyileştirmelerine yardımcı olur. Her bir metriği ve yöntemi anlamak, makine öğrenimi projelerinizde daha bilinçli kararlar vermenize ve başarıya ulaşmanıza yardımcı olur.